jueves, 17 de septiembre de 2020
viernes, 19 de junio de 2020
ESTADÍSTICA Y PROBABILIDAD.
Frecuencia absoluta y frecuencia relativa
Cuando se escribe una tabla para anotar los datos que se obtuvieron de algún evento, experimento aleatorio o juego de azar, se está haciendo un estudio estadístico.
La frecuencia es el número de veces que se repite un valor o dato de análisis en una tabla.
Hay dos tipos de frecuencia: la absoluta y la relativa.
La frecuencia absoluta es el número de veces que se repite cada dato y la frecuencia relativa se obtiene dividendo la frecuencia absoluta entre el total de registro.
La frecuencia relativa nos ayuda a identificar tendencias. El número cuya frecuencia se acerque más a la unidad es el que tiene mayores probabilidades de salir.
En la tabla de frecuencias absolutas es sencillo visualizar cómo se distribuyen los datos.
La columna de las frecuencias absolutas nos indica el número de veces que ocurre un mismo dato.
Ejemplo:
La frecuencia de los alumnos que miden 1.60 m es 1; la frecuencia de los alumnos que miden 1.55 m es 2, etcétera.
Estatura
|
Frecuencias
|
1.60 m
|
1
|
1.55 m
|
2
|
1.50 m
|
10
|
1.45 m
|
15
|
1.40 m
|
2
|
1.35 m
|
3
|
1.30 m
|
1
|
1.25 m
|
1
|
Total
|
35
|
Después de analizar la información de los resultados, podemos responder las siguientes preguntas:
¿Cuál es la frecuencia de los alumnos que miden 1.45?
R = 15
¿Cuál es la frecuencia de los alumnos de 1.30?
R = 1
¿Cuántos integran el grupo?
R = 35
¿Cuántos miden menos de 1.40?
R = 5
¿Cuál es la diferencia de estatura entre el más alto y el más bajo?
R = 0.35 m
En una tabla la suma de todas las frecuencias relativas debe dar como resultado 1.00 (un entero). La frecuencia relativa se puede expresar en fracciones, en números decimales o porcentajes.
Actividades de repaso:
- Estadística: Frecuencia absoluta y frecuencia relativa.
- Frecuencia y probabilidad.
- Tablas y gráficos estadísticos.
Media aritmética
La media aritmética es el valor obtenido al sumar todos los datos y dividir el resultado entre el número total de datos.
La moda
La moda es el valor con una mayor frecuencia en una distribución de datos.
La mediana
- La mediana de un conjunto ordenado de un número de elementos impar es aquel que ocupa el lugar central.
5 7 12 13 15
mediana
- La mediana de un conjunto ordenado de un número de elementos par es la media aritmética de los dos valores que ocupan el lugar central.
5 7 9 12 13 15
9 + 12 = 10,5 (mediana)
2
- El rango, en un conjunto ordenado de números, es la diferencia entre el valor mínimo y el valor máximo.
5 7 9 12 13 15
El rango es: 15 - 5 = 10
- Actividades de repaso:
lunes, 1 de junio de 2020
MEDIDA.
UNIDADES DE MEDIDA DE LONGITUD
- Actividades de repaso:
- Medidas de longitud I.
- Medidas de longitud II.
- Unidades de longitud. Relaciones.
- Repaso unidades de longitud.
UNIDADES DE MEDIDA DE CAPACIDAD
- Actividades de repaso:
- Unidades de capacidad. Relaciones.
- Unidades de capacidad. Relaciones II.
- Medidas de capacidad I.
- Medidas de capacidad II.
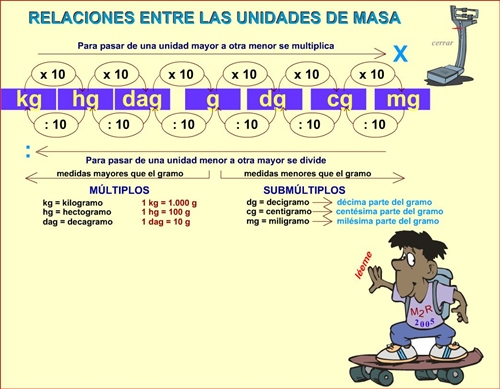
UNIDADES DE MEDIDA DE MASA
1 Tonelada = 1000 Kg.
- Actividades de repaso:
- Unidades de masa I.
- Unidades de masa II.
- Unidades de masa III.
- Problemas de unidades de masa.
- La masa.
SISTEMA SEXAGESIMAL
1.- UNIDADES DE TIEMPO:
* Segundo (s) * Minuto (min) * Hora (h)
* Día * Semana * Mes
* Año * Lustro * Década
* Siglo * Milenio
2.- EQUIVALENCIAS ENTRE UNIDADES DE TIEMPO:
1 minuto = 60 segundos
1 hora= 60 minutos = 3.600 segundos
1 día = 24 horas
1 semana = 7 días
1 mes = 30 días (hay de 28 y de 31, pero para los problemas se consideran de 30 días)
1 año = 365 días = 52 semanas
1 lustro = 5 años
1 década = 10 años
1 siglo = 100 años
1 milenio = 1.000 años
- Actividades de repaso:
UNIDADES DE MEDIDA DE ÁNGULOS
 El ángulo es la región del plano comprendida entre dos rectas que se unen en un mismo punto llamado origen. Los ángulos se calculan siempre en sentido contrario a las agujas del reloj.
El ángulo es la región del plano comprendida entre dos rectas que se unen en un mismo punto llamado origen. Los ángulos se calculan siempre en sentido contrario a las agujas del reloj.- Actividades de repaso:
SUMA Y RESTA EN EL SISTEMA SEXAGESIMAL
SUMA
1 Se colocan las horas debajo de las horas (o los grados debajo de los grados), los minutos debajo de los minutos y los segundos debajo de los segundos; y se suman.
2 Si una vez sumados los segundos son más de 60 se pasan a minutos. Si una vez sumados los minutos son más de 60 se pasan a horas.
RESTA
1 Se colocan las horas debajo de las horas (o los grados debajo de los grados), los minutos debajo de los minutos y los segundos debajo de los segundos.
Ejemplo:

2 Se restan los segundos. Caso de que no sea posible, convertimos un minuto del minuendo en 60 segundos y se lo sumamos a los segundos del minuendo. A continuación restamos los segundos.
Ejemplo:

3 Hacemos lo mismo con los minutos. Y después restamos las horas.
Ejemplo:

UNIDADES DE MEDIDA DE SUPERFICIE
Medidas de superficie:
Problema de superficies:
- Actividades de repaso:
lunes, 25 de mayo de 2020
PROPORCIONALIDAD Y PORCENTAJES
Magnitudes proporcionales
Dos magnitudes son proporcionales si las dos magnitudes aumentan o disminuyen en la misma proporción.
La misma variación que experimenta la primera cantidad se le aplica a la segunda.
Por ejemplo:
Si vas al cine una entrada cuesta 9 euros, si compras más entradas te costará más dinero.
Luego si compramos 3 entradas nos costará 9 x 3 = 27 euros.
Porque multiplicamos al número de entradas y al dinero por el mismo número, en este caso es 3.
Por este motivo decimos que el número de entradas
y el dinero que cuesta son magnitudes proporcionales.
Otro ejemplo:
Si una camisa cuesta 20 euros ¿Cuento cuestan 6 camisas?
El número de camisas se ha multiplicado por 6, luego el precio también habrá que multiplicarlo por 6:
20 x 6 = 120
Las 6 camisas cuestan 120 euros.
Actividades de repaso
El porcentaje o tanto por ciento
En matemáticas, el porcentaje es una forma de expresar un número como una fracción que tiene el número 100 como denominador. También se le llama comúnmente tanto por ciento, donde por ciento significa «de cada cien unidades» El porcentaje se denota utilizando el símbolo %.
El porcentaje de una cantidad

Actividades de repaso
- Descuentos y aumentos de una cantidad
Para realizar descuentos
se puede calcular primero la cantidad a descontar y luego restar esta
cantidad al valor inicial.
Es decir, primero calculamos el porcentaje de la cantidad y luego se lo restamos al valor que teníamos inicialmente.
Para realizar aumentos se puede calcular primero la cantidad a aumentar y luego sumar esta cantidad al valor inicial.
Es decir, primero calculamos el porcentaje de la cantidad y luego se lo sumamos al valor que teníamos inicialmente.
Actividades de repaso
Planos y mapas
- Los planos y los mapas.

Mientras que los mapas son representaciones gráficas, a tamaño reducido de grandes superficies, como una provincia, un país o un continente.
Por lo que las diferencias son las siguientes:
- Planos: para localizar casas, parques, calles.
- Mapa: para localizar países, ciudades, montañas o ríos.
- Escala numérica y escala gráfica:
Actividades de repaso:
- Importancia de los mapas:
lunes, 18 de mayo de 2020
DIVISIÓN DE NÚMEROS DECIMALES
División por la unidad seguida de ceros
División de un decimal entre un natural
Ejemplo:
ACTIVIDADES DE REPASO
División de un decimal entre un natural
Para dividir un número decimal entre uno natural se realiza la división como siempre,pero cuando llega la el momento de bajar el número que viene después de la coma ponemos una coma en el cociente.
EJEMPLO:
2,6 I_2___ --> 2,6 I_2___ --> 2,6 I_2___
0 1 0 6 1,3 0 6 1,3
0
ACTIVIDADES DE REPASO:
División de un natural entre un decimal
Para dividir un número natural por un número decimal eliminas la coma del divisor y escribes a la derecha del dividendo tantos ceros como cifras decimales tiene el divisor y haces la división como si fueran números enteros y positivos.
Ejemplo:
12 : 2,6
(12 x 10) : (2,6 x 10)
120 : 26
4,61
ACTIVIDADES DE REPASO:
División de un decimal entre un decimal
Para dividir un número decimal entre un número decimal, se multiplican ambos por la unidad seguida de tantos ceros como cifras decimales tenga el divisor, y después se hace la división obtenida.
Lo importante es saber que el dividendo de la división obtenida puede ser un número natural o decimal, pero el divisor siempre es un número natural.
ACTIVIDADES DE REPASO:
- División de un número decimal entre un decimal.
- División con números decimales I.
- División con números decimales II.
- El tesoro de la gruta.
Aproximación de cocientes con cifras decimales
En una división entera, se puede aproximar el cociente con tantas cifras decimales como se desee, escribiendo el dividendo con ese mismo número de cifras decimales.
ACTIVIDADES DE REPASO:
Expresión decimal de una fracción
Toda fracción tiene una expresión decimal que se obtiene dividiendo su numerador entre su denominador.
Suscribirse a:
Entradas (Atom)

















.jpg)